- RL Course by David Silver
- Lecture 1: Introduction to Reinforcement Learning
- Lecture 2: Markov Decision Process
RL Course by David Silver
#Lecture 1: Introduction to Reinforcement Learning
两本书推荐
- An Introduction to Reinforcement Learning, Sutton and Barto, 1998 概念多一些
- Algorithms for Reinforcement Learning, Szepesvari 数学细节多一些
都有免费的online版本
什么是强化学习
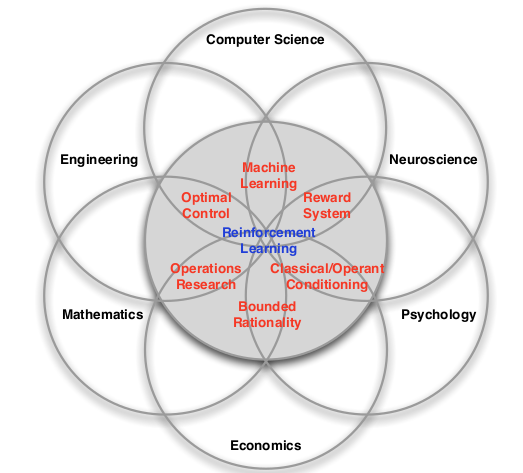
多种交叉的学科
RL的特点
- no supervisor, only a reward signal
- Feddback is delayed, not instantaneous
- time really matters(连续的处理)
- Agent’s actions affect the subsequent data it receives(与环境产生交互)
强化学习
每个时刻都有一个$R_t$,表示t时刻的reward。强化学习的目标就是最大化$R_t$。
example of reward
- Fly stunt manoeuvres in a helicopter
- +ve reward for following desired trajectory
- −ve reward for crashing
- Defeat the world champion at Backgammon
- +/−ve reward for winning/losing a game
- Manage an investment portfolio
- +ve reward for each $ in bank
- Control a power station
- +ve reward for producing power
- −ve reward for exceeding safety thresholds
- Make a humanoid robot walk
- +ve reward for forward motion
- −ve reward for falling over
目标:选择最大化$R_t$的action
- action可能影响时间很长
- 可能会延迟
- 可能需要放弃一些暂时的reward
Agent and Environment
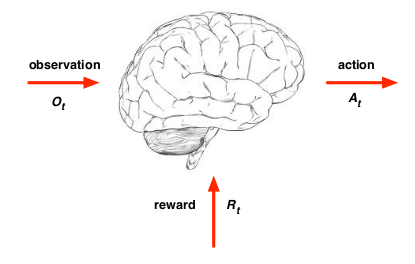
在每个时间,对于agent而言
- 执行动作$A_t$
- 收到环境信息$O_t$
- 收到reward$R_t$
在每个时间,对于enviroment而言
- 收到动作$A_t$
- 发出$O_t$
- 发出$R_t$
History and State
history: $H_t = O_1,R_1,A_1,…A_t-1,O_t,R_t$
将要发生的事情,取决于$H_t$
State是信息的summary $S_t = f(H_t)$
State
environment state $S_t^e$
environment对于agent是不可见的,即使可见也包含不相干的内容
agent state $S_t^a$
可以是$H_t$的任意函数 $S_t^a = f(H_t)$
information state(a.k.a Markov state) 含有所有的历史有信息,是个信息论的该你那 当下面条件满足的时候$S_t$是 Markov $P[S_{t+1}|S_t]=P[S_{t=1}|S_1,..,S_t]$
-
未来与过去是独立的 $H_{1:t} –> S_t –> H_{t+1: \infty}$
- 一旦state确定了,所有的history都可以被丢弃
- environment state $S_t^e$ 是 Markov
- history of everything $H_t$是Markov
例子
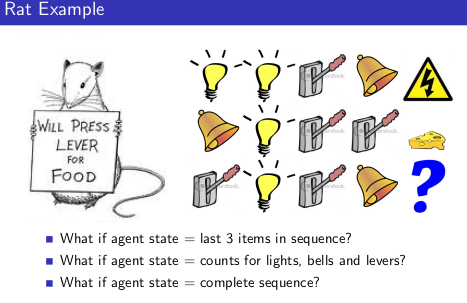
full Observable
$O_t = S_t^a=S_t^e$ 即可以观察到所有情况,这是个 Markov decision process(MDP)
Partal observability
agent state != environment state
通常这是个 partially observable Markov decision process(POMDP)
这样agent需要有自己的state,例如
- 完整的历史$S_t^a = H_t$
- 对环境状态分布的估计$S_t^a =(P[s_t^e=s1],…,p[S_t^e=s_n])$
- RNN $S_t^a = \sigma(S_t-1^a W_S +O_tW_o)$
RL agent的组成
下面这些并不一定是都是必要的
- Policy agent如何选择action
- Value function 如何评价一个state或者是action
- Model 表示environment
policy
policy是agent的行为 他是state到action的映射 确定的policy $a=\pi(s)$ 随机的policy $\pi(a|s)=P[A_t=a|S_t=s]$
Value function
评估action
| $V_{\pi}(s)=E_\pi[R_t+\gamma R_{t+1}+\gamma ^2 R_{t+2} | S_t=s]$ |
model
model预测环境
$P$预测next state
$R$预测 next(immediate) review
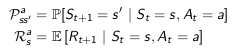
例子

RL分类
- Value Based
- No policy(implicit)
- Value Function
- Policy Base
- Policy
- No value Function
- Actor Critic 结合两者
- Policy
- Value Function
- Model Free
- Policy and/or ValueFunction
- No model
- Model base
- Policy and/or value function
- model

Learning and Planning
- 强化学习
- 环境不可知
- agent与环境交互
- 提升policy
- Planning
- model可知
- agent的行为可由model得到
- agent提升policy
- a.k.a. deliberation, reasoning, introspection, pondering, thought, search 更像搜索
balance Exploration and Exploitation
Exploitation: 最大化以知最优 Exploration:最大化经验化环境
例子:
- Restaurant Selection
- Exploitation Go to your favourite restaurant
- Exploration Try a new restaurant
- Online Banner Advertisements
- Exploitation Show the most successful advert
- Exploration Show a different advert
- Oil Drilling
- Exploitation Drill at the best known location
- Exploration Drill at a new location
- Game Playing
- Exploitation Play the move you believe is best
- Exploration Play an experimental move
Prediction and Control
预测:Given a policy,衡量它 控制:选择最好的策略
总结
- $O_t,R_t,A_t$ 表示的是agent与环境的交互
- $H_t$,$S_t$ 表示的是历史的提炼
- $S_t$ 是 Markov 可以理解为信息足够,可以进行推断
- agent中model,policy,value funcion和分类
- 强化学习用于解决不同的问题,Learning和Planing,Prediction和Control,Exploration and Exploitation
Lecture 2: Markov Decision Process
Markov Processes
Introduction
- Almost all RL problems can be formalised as MDPs
Markov Property
- state是有足够的统计量用于预测未来

### Markov Chains
Markov Process(or Markov Chain)
S 是一组状态 P 是状态转移概论矩阵 $P_{ss’}=P[S_{t+1}=s’|S_t=s]$
### Example: Student Markov Chain
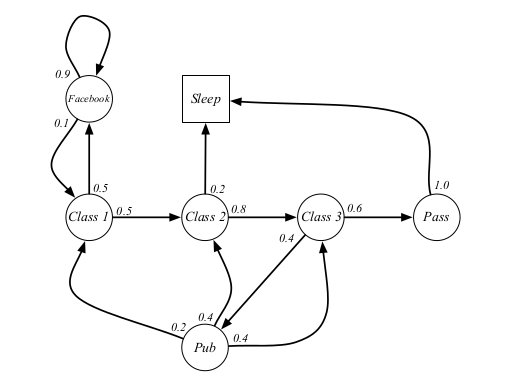
进行sample 有这些可能的序列
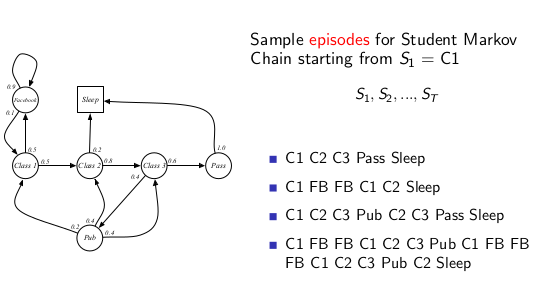
Transition Matrix
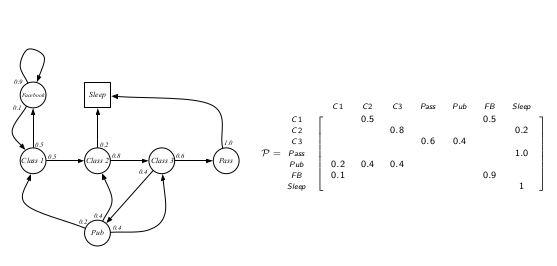
Markov Reward Process
带有value judgement的 Markov 过程
S 是一组状态 P 是状态转移概论矩阵 $P_{ss’}=P[S_{t+1}=s’|S_t=s]$ $R_s=E[R_{t+1}|S_t=s]$
### Student MRP

### return G: Goal $G_t=R_{t=1}+\gamma R_{t+2}=\sum_{k=0} \gamma^k R_{t+k+1}$
$\gamma$ 是 discount 属于 [0,1] $\gamma$ 接近0 会比较贪心,接近1则会导致比较长远的进化
为什么使用discount
- 数学上方便
- 防止Markov process中的环
- 没有环境的完美model,所与更远的reword,占比更小
- 人和动物都对马上发生的事情反映
- 如果在经济上,表示了interest
- 如果知道序列会终止,可以不使用discount
Value Function
| $v(s)=E[G_t | S_t=s]$ |
如果你从state s开始,Goal是什么。
Example
$S_1=C_1$做sample,然后按照公式计算,gamma取0.5

gamma取0
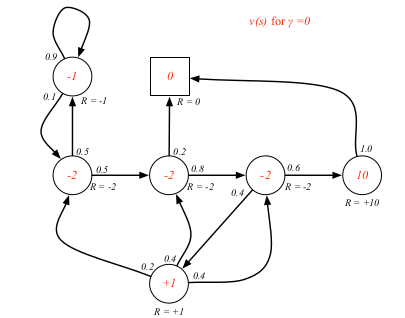
gamma取0.9
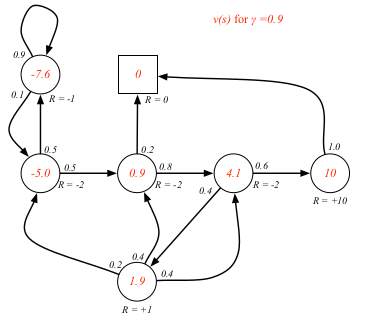
### Bellman Equation
value function 由两部分组成
- 立刻的reward $R_{t+1}$
- discounted 的 接下来的状态$\gamma v(S_{t+1})$
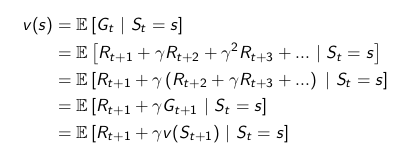
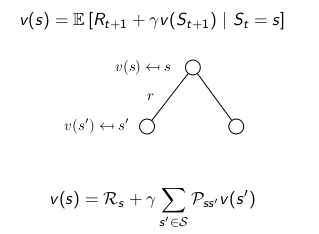
### Example
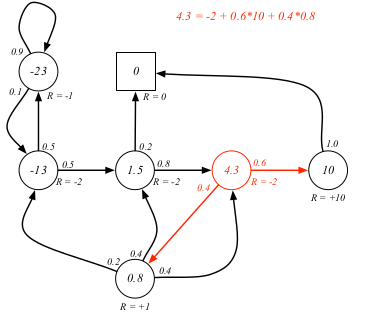
### Bellman Equation in Matrix Form
$v = R + \gamma P v$ R 马上的回报
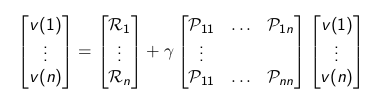
### Solving the Bellman Equation

MDP Markov Decision Process
马尔科夫过程是一个元组$S,A,P,R,\gamma$
$S$ 是一组有限的states集合 $A$ 是一组有限的action集合 $P$ 是一个状态转换概率矩阵 $P_{ss’}^a=P[S_{t+1}=s|S_t=s,A_t=a]$ $R$是reward function,$R_s^a=E[R_{t+1}|S_t=s,A_t=a]$ $\gamma$ 是 discount factor
例子
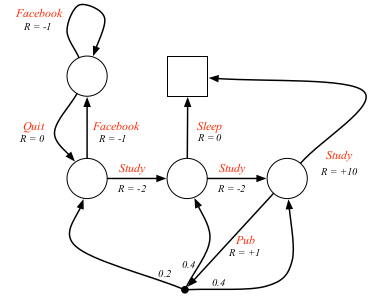
### policy
A policy π is a distribution over actions given states, $π(a|s) = P [A_t = a | S_t = s]$
- policy 具有对于agent行为的完全的定义
- 在MDP中,action只基现在的状态

### Value Function state-value function: 从s状态,遵从policy pi 的 期望
| $v_π (s) = E_π [G_t | S_t = s]$ |
action-valute function:
在s 状态,采取a操作,然后遵从policy pi 的期望
| $q π (s, a) = E π [G t | S t = s, A t = a]$ |
### value function example
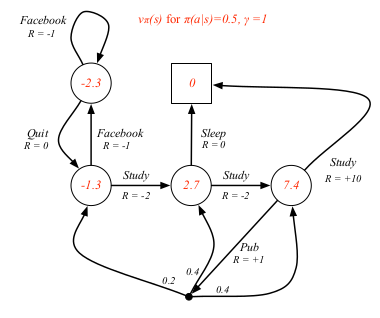
### Bellman Expectation Equation

### Bellman Expectation Equation
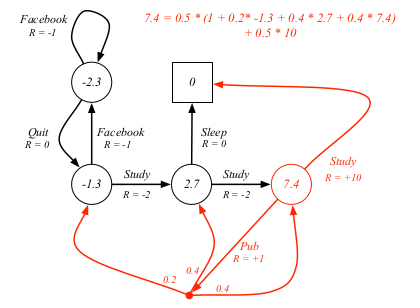
## Optimal Value Function
在所有的policies下有可能获得的最大值 $v_∗ (s) = \max v_π (s)$ π
在action下能获得的最大数值 $q_∗ (s, a) = \max q_π (s, a)$
- optimal value fn 表明了MDP有可能的最好性能
- 如果optimal value fn能够被知道,那么MDP就被”解决了”
Example Optimal value fn
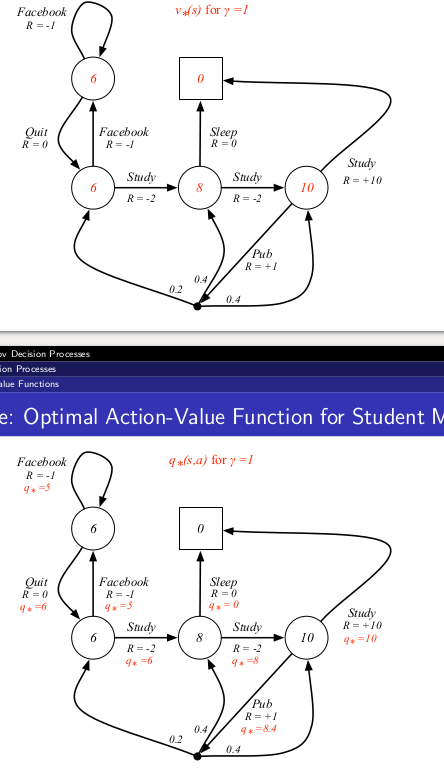
## Optimal Policy
$π ≥ π’ if v_π (s) ≥ v_{π’}(s), ∀s$
### Example Optimal Policy
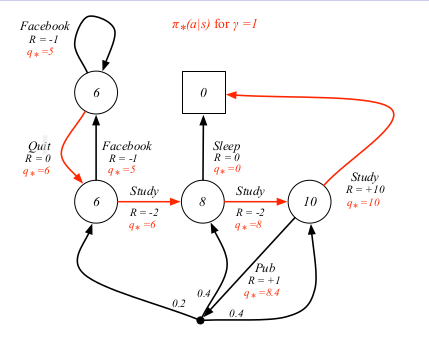
## 如何计算
- Bellman 优化等式是非线性的
- 没有近似的solution
- 采用迭代的方法
- Value iteration
- Policy Iteration
- Q-learning
- Sarsa