RL Course by David Silver
Lecture 3: Planing by Dynamic Programming
Inroduction
DP是什么
这里不是特指编程里面的DP
- 把复杂问题分解为子问题
- 解决子问题
- 把子问题的解决结合起来
DP的需要满足的条件
- 可以分解为子问题
- 子问题重复重现,可以被存储和重用
- Markov decision process满足这两个条件
Planning by DP
预测问题
- Input: $MDP<S, A, P, R, γ_i >$ and policy π
- Output: value function$v_\pi$
控制问题
- Input: $MDP<S, A, P, R, γ_i >$
- Output: optimal value function and optimal policy
Policy Evaluation
评估给定的policy $\pi$
example
问题定义
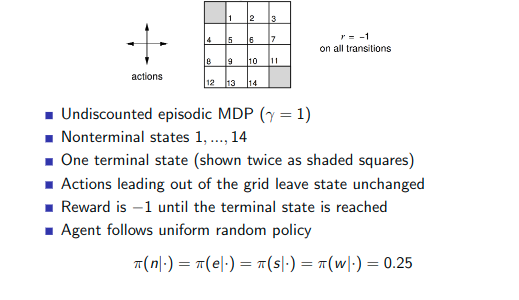
过程
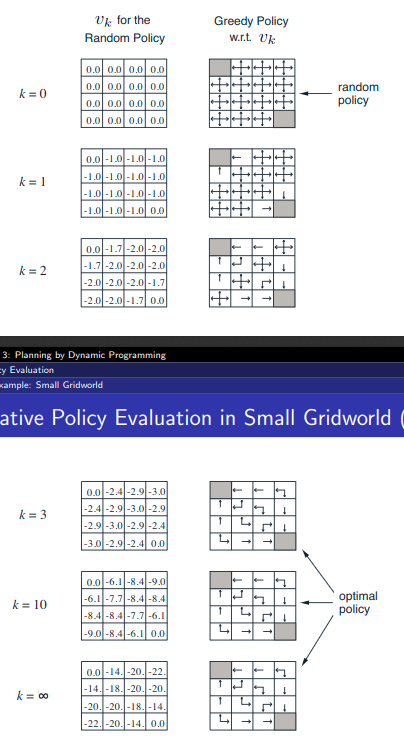
-
左边的图计算过程:上一步的状态+当前这一步的状态
-
右边的policy得到的结果,根据左边的分数得到
获取最好的policy
给定一个policy $\pi$
- Evaluate the policy $v_\pi(s)=E[R_{t+1}+\gamma R_{}]$
- $\pi’=greedy(v_\pi)$
使用获得最高value的action
虽然更多的iteration可以提高policy,但是它最终是收敛的。
为什么是收敛的,为什么是最优policy

这个过程中

如果提升停止了,那么Bellman optimality equation就被满足了,所以此时的$\pi$是最优 policy
如何stop early
因为没必要找到最优的 value 才能获得最优的 policy
- n个迭代
- 引入停止条件
- 不是每次都更新
Principle of Optimality

总结
- 问题:找到最优的policy $\pi$
- Solution:迭代的使G用Bellman优化 backup
- $v_1 -> v_2 -> v_3 … -> v_*$,找到最优的value
- 使用同步backup
- 在每个k+1迭代
- 对于所有s
- 从$v_k(s’)$中更新$v_k(s’)$
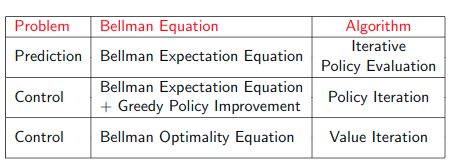
扩展dp
异步backups
Ideas
- in-place dp
- Prioritiesed sweeping
- Real-time dynamic programming
in-place dp

Prioritised Sweeping
找到那个state变化最快

Real-Time Dynamic Programming

完整的backup
 sample的backup
sample的backup

lecture 4:Model-Free Predction
在不知道环境具体怎么行为的前提下,如何直接通过agent和env的交互评估一个策略的好坏,或者寻找到一个最优的策略。
本章主要讲策略评估,也就是预测问题。
蒙特卡洛强化学习
蒙特卡洛方法(MC)又称之为经验统计方法,它有以下特点
- 直接从序列中学习。
- 无需model,无需知道MDP的转移和回报。
- 直接从整个序列中学习,序列可以从任意点开始,并且不需要进行引导(bootstrap)
- 但是所有的序列都必须有终止。
使用MC来评估一个策略
给予策略$\pi$的一个Episode表示如下:
$S_1,A_1,R_2,…,S_t,A_t,R_{t+1},..,S_k \backsim \pi$
t时刻的Gain为 $G_t = R_{t+1} + \gamma R_{t+2} + … +\gamma^{T-1}R_T$,T为终止时刻。
那么状态s的价值表示为
| $v_\pi(s)=E_\pi(G_t | S_t=s)$ |
first visit 和 every visit
由于在序列中很有可能会包含同一个状态,有两种方法选择。
first visit
只把第一次出现这个状态纳入到收获平均值的计算中
every visit
把每一次出现这个状态都纳入平均值计算
Example 21点
States (200 of them):
- Current sum (12-21)
- Dealer’s showing card (ace-10)
- Do I have a “useable” ace? (yes-no)
Action
- stick: Stop receiving cards (and terminate)
- twist: Take another card (no replacement)
Reward for stick:
- +1 if sum of cards > sum of dealer cards
- 0 if sum of cards = sum of dealer cards
- -1 if sum of cards < sum of dealer cards
Reward for twist:
- -1 if sum of cards > 21 (and terminate)
- 0 otherwise
Transitions:
- automatically twist if sum of cards < 12
累进更新平均值
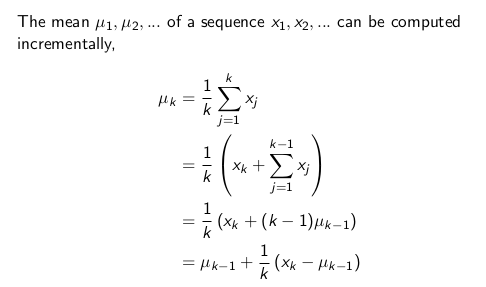
累进更新平均值用于蒙特卡洛中。
时序差分强化学习
TemporalDifference Learning(TD)
特点:
- model-free
- 从不完整的序列开始,需要合理的引导(bootstrapping)
- TD updates a guess towards guess
TD表示
$V(S_t) \larr V(S_t) + \alpha ((R_{t+1}+\gamma V(S_t+1))-V(S_t))$
其中$R_{t+1}+\gamma V(S_t+1)$是TD的目标值,$R_{t+1}+\gamma V(S_t+1)-V(S)_t$称之为TD误差
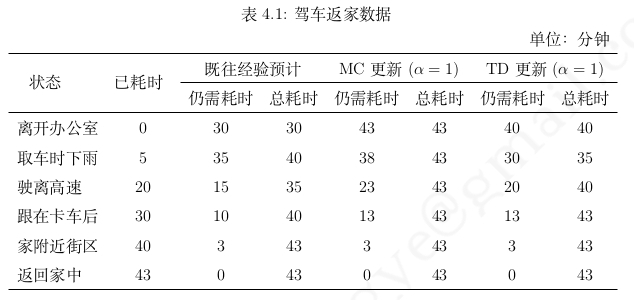
MC和TD例子
这个例子中没有action,没有policy reward_function是time_take
只考虑reward function
MC与TD优点
- mc是$v_\pi(S_t)$的无偏估计
- TD target是$v_\pi(S_t)$的有偏差估计
- 可以用于没有结束的spisode
- 在最终结果出来就可以学习
例子
有 8 个 episodes A, 0, B, 0 B, 1 B, 1 B, 1 B, 1 B, 1 B, 1 B, 0
what is V(A),V(B)
使用MC计算,因为只有一个序列包含A,
$V(A)=G(A) = R_A + \gamma R_B $
$V(B) = 6/8$
MC算法直接依靠完整序列的奖励的各个状态对应的收获来计算,这种算法是最小化收获与状态价值之间的方差为目标
$\sum^K_{k=1}\sum^{T_k}_t(G^k_t-V*S^k_t)$
使用TD计算,
$V(B) = 6/8$ $V(A) = 6/8$
TD试图构建一个$MDP(S,A,\hat P,\hat R,\gamma)$,这个MDP尽可能符合已经产生的序列,也就是说TD算法首先根据已有的经验估计状态转移概率
$\hat P^a_{s,s’}=\frac 1 N(s,a) \sum^K_{k=1}\sum^{T_k}{t=1}(S^k_t,a^k_t,S^k{t+1} = s,a,s’)$
$\hat R^a_{s,s’}=\frac 1 N(s,a) \sum^K_{k=1}\sum^{T_k}_{t=1}(S^k_t,a^k_t = s,a)$
区别
MC
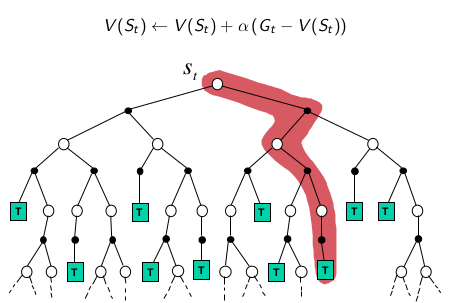
MC采用深采样,一次完整的经历,使用实际收获更新状态估计值。
TD
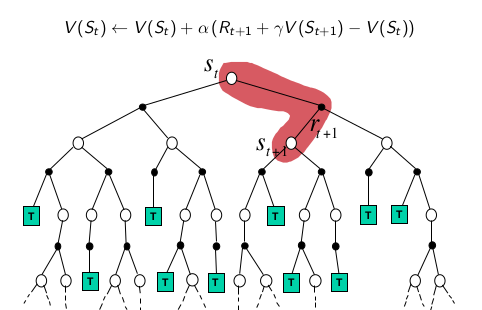
TD采用浅层采样。使用后续状态的预估状态价值预估收获在更新当前状态价值。
DP
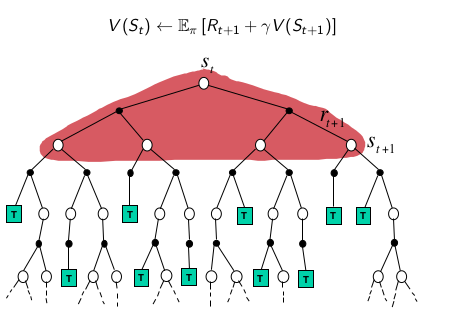
DP使用全部后续状态预估值更新当前状态
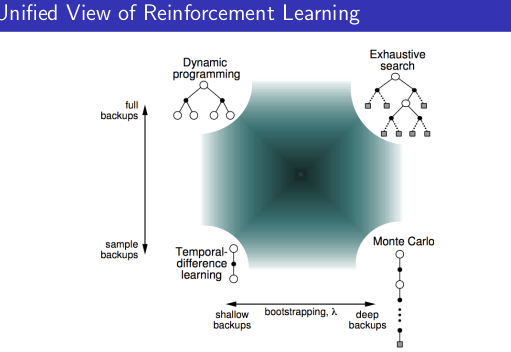
综合上述三种学习方法的特点,可以小结如下:当使用单个采样,同时不经历完整的状态序 列更新价值的算法是 TD 学习;当使用单个采样,但依赖完整状态序列的算法是 MC 学习;当 考虑全宽度采样,但对每一个采样经历只考虑后续一个状态时的算法是 DP 学习;如果既考虑所 有状态转移的可能性,同时又依赖完整状态序列的,那么这种算法是穷举 (exhausive search) 法。 需要说明的是:DP 利用的是整个 MDP 问题的模型,也就是状态转移概率,虽然它并不实际利 用采样经历,但它利用了整个模型的规律,因此也被认为是全宽度 (full width) 采样的。
n步时序差分学习,

从公式 4.4,4.5 可以得到,当 n=1 时等同于 TD(0) 学习,n 取无穷大时等同于 MC 学习。 由于 TD 学习和 MC 学习又各有优劣,那么会不会存在一个 n 值使得预测能够充分利用两种学 习的优点或者得到一个更好的预测效果呢?研究认为不同的问题其对应的比较高效的步数不是 一成不变的。选择多少步数作为一个较优的计算参数是需要尝试的超参数调优问题。
从 n=1 到 ∞ 的所有步收获的权重之和。其中,任意一个 n-步收获的权重被设计为 (1 − λ)λ n−1 ,如图 4.7 所示。通过这样的权重设计,可以得到 λ-收获的计算公式为:

向前TD与向后TD
Lecture 5 Model-Free Control
- 参考笔记,这个笔记不错 https://zhuanlan.zhihu.com/p/37690204